离散数学 笔记

上半学期

Lec1

• $\mathbb{Q}$: 有理数
• 基本代数定理 FTA：任何大于1的整数都能被分解为质数乘积 $n=p_1^{e_1}\cdots p_r^{e_r}$（数学归纳法证明）
• 良序公理：非空非负子集有最小元
• 带余除法：$a=bq+r$
• 理想：加法/数乘封闭，$d\mathbb{Z}=\{0,\pm d,\pm 2d,\cdots\}$，$a\mathbb{Z}+b\mathbb{Z}=\gcd(a,b)\mathbb{Z}$
• $\gcd(a,b)=p_1^{min(\{\alpha_1,\beta_1\})}\cdots p_r^{min(\{\alpha_r,\beta_r\})}$
• 裴蜀定理 Bézout’s Theorem：$\exists s,t\in\mathbb{Z},\gcd(a,b)=as+bt$

Lec2

• 二元关系：是 $A\times B$ 的子集 $R$，$aRb$ 意味着 $(a,b)\in R$
• 等价关系：$R$ 在 $A$ 上，满足 $\forall a\in A,aRa$（自反性），对称性，传递性的集合
• 等价类：$[a]_R=\{b\in A:aRb\},a\in A$
• 剩余类：$[a]_n=a+n\mathbb{Z}=\{a+nx:x\in Z\}$（$a\bmod n$ 下的）
• $\mathbb{Z}_n=\{[0]_n,[1]_n,\cdots,[n-1]_n\}=\{0,1,\cdots,n-1\}$

Lec3

• $[b]_n[s]_n=[1]_n$，则 $[s]_n$ 为 $[b]_n$ 逆元（EEA求解）
• $\mathbb{Z}_n^*=\{[b]_n\in\mathbb{Z}_n:\gcd(b,n)=1\}$（与 $n$ 互质；是循环群，所有元素都是生成元）
• 欧拉 $\phi$ 函数：$\phi(n)=|\mathbb{Z}_n^*|=n(1-p_1^{-1})\cdots(1-p_r^{-1})$
• 欧拉定理：$n \le 1, \alpha \in \mathbb{Z}_n^*$，则 $\alpha^{\phi(n)}=1$
• 费马小定理：在欧拉定理基础上取 $n$ 为质数，即 $\alpha^{p-1}=1$

Lec4

• RSA：取质数 $p,q,N=pq,r=\phi(N)$，选择整数 $e,e<r,\gcd(e,r)=1$，求其逆元 $d=e^{-1}\bmod r$
• 公钥 $(N,e)$ 私钥 $(N,d)$，$m\rightarrow c:=m^e\bmod N\rightarrow m=c^e\bmod N$

Lec5

• 二进制加减法：$O(k)$，乘法：$O(k^2)$，除法：$O((k-l+1)\cdot l)$，快速幂：$O(k)$
• 乘法：和快速幂同一种算法；除法：先令余数 $r:=a$，再模拟竖式计算

Lec6

• 扩展欧几里得算法（EEA）：求解 $as+bt=\gcd(a,b)$，$r_0=a,r_1=b$，复杂度 $O(l(a)l(b))$

$$\begin{array}{|c|c|c|c|c|} \hline i & r_i & q_i & s_i & t_i \\ \hline 0 & 12345 & & 1 & 0 \\ 1 & 123 & 100 & 0 & 1 \\ 2 & 45 & 2 & 1 & -100 \\ 3 & 33 & 1 & -2 & 201 \\ 4 & 12 & 2 & 3 & -301 \\ 5 & 9 & 1 & -8 & 803 \\ 6 & 3 & 3 & 11 & -1104 \\ 7 & 0 & & & \\ \hline \end{array}$$

• （疑似不重要）素数理论：$\pi(x)$ 为小于等于 $x$ 素数个数，有 $\lim_{x\to\infty}\frac{\pi(x)}{\frac{x}{\ln x}}=1$；$\mathbb{P}_n$ 为 $2^{n-1}$ 到 $2^n$ 素数个数，则 $|\mathbb{P}_n|\ge \frac{2^n}{n\ln2}(\frac{1}{2}+O(\frac{1}{n}))$；说明生成素数的高效性

Lec7

• 线性同余方程：$d:=\gcd(a,n),ax\equiv b\pmod n$ 有解 $\Leftrightarrow d\mid b$（裴蜀定理，即 $b=k\gcd(a,n)$）
• $d:=\gcd(a,n),t:=(\frac{a}{d})^{-1} \bmod \frac{n}{d},d \mid b$ 则 $ax\equiv b\pmod n \Leftrightarrow x \equiv \frac{b}{d}t \pmod {\frac{n}{d}}$（约分）
• 中国剩余定理：$\{x \equiv b_i \pmod{n_i}$ 任意 $n_i$ 互质，则有解
• 先求 $n=\prod n_i$，记 $N_i=\frac{n}{n_i}$，由 $s_iN_i+t_in_i=1$ 用 EEA 求出 $s_i$，令 $b=\sum b_i(N_is_i)$，得解 $[b]_n$
• CRT 映射：$k$ 个两两互质正整数，$n=\prod n_i$，则映射 $\theta([x]_n)=([x]_{n_1},\cdots,[x]_{n_k})$ 为 $\mathbb{Z}_n$ 到 $\mathbb{Z}_{n_1}\times\cdots\times\mathbb{Z}_{n_k}$ 以及 $\mathbb{Z}_n^*$ 到 $\mathbb{Z}_{n_1}^*\times\cdots\times\mathbb{Z}_{n_k}^*$ 的双射
• 良定义：$[x]_n=[y]_n\Rightarrow\theta([x]_n)=\theta([y]_n)$；单射：$\theta([x]_n)=\theta([y]_n)\Rightarrow[x]_n=[y]_n$
• 欧拉 $\phi$ 函数：若 $n=n_1\cdots n_k$，且 $n_i$ 两两互质，则 $\phi(n)=\phi(n_1)\cdots\phi(n_k)$；若 $n_i$ 均为质数，则 $\phi(n)=(p_1^{e_1}-p_1^{e_1-1})\cdots(p_k^{e_k}-p_k^{e_k-1})=n(1-p_1^{-1})\cdots(1-p_k^{-1})$

Lec8

• 群：封闭性 Closure、结合律 Associative、单位元 Identity ($a*e=e*a=a$)、逆元 Inverse ($a*b=b*a=e$)；阿贝尔群：交换律
• $(\mathbb{Z}_n,+)$：阿贝尔群，单位元为 $[0]_n$；$(Z_n^*,\cdot)$：当 $n>1$ 时为阿贝尔群
• 阶 Order：群的阶是群的元素个数；群内元素 $a$ 的阶是使得 $a^l=1$ 的最小 $l$（加法群为 $la=0$）
• 若乘法阿贝尔群阶数为 $m$，则对于任意 $a\in G$，都有 $a^m=1$
• 子群：$(G,\cdot)$ 是阿贝尔群，令 $g\in G,\langle g \rangle = \{g^k:k\in\mathbb{Z}\}$ 为 $G$ 的子群，且 $\langle g \rangle \le G$
• 循环群 Cyclic Group：$\langle g \rangle = G$，则 $g$ 为 $G$ 的生成元；对于质数 $p$，$\mathbb{Z}_p^*$ 为循环群

Lec9

• DLOG：循环群内若 $h=g^x$，则 $x=\log_g h$，称 $x$ 为 $h$ 的离散对数
• 若安全素数 $p=2q+1$，$q$ 也为素数，则难以计算 DLOG：$\exp(O(\sqrt{\ln q\ln\ln q}))$
• Diffie-Hellman Key Exchange：A, B 规定大素数 $p$ 以及生成元 $g$，使得 $G=\langle g \rangle$ 的阶为 $p$；A 选择 $a\leftarrow \mathbb{Z}_p,A=g^a$ 发送给 B；B 选择 $b\leftarrow\mathbb{Z}_p,B=g^b$ 发送给 A；则密钥 $k=B^a=A^b=g^{ab}$

Lec10

• 集合的基数 Cardinality：若是有限集，则为元素个数
• 两个任意集合 $A,B$ 有相同基数（$|A|=|B|$）当存在双射 $f:A\rightarrow B$
• 当存在单射 $f:A\rightarrow B$，则 $|A|\le|B|$；同时满足 $|A|\ne|B|$ 时则 $|A|<|B|$
• $|\mathbb{Z}^+|=|\mathbb{N}|=|\mathbb{Q}^+|=|\mathbb{Q}|,|\mathbb{R}^+|=|\mathbb{R}|=|(0,1)|=|[0,1]|$
• 证明 $|(0,1)|=|[0,1]|$：取 $f(0)=2^{-2},f(1)=2^{-1},f(2^{-n})=2^{-n-2}$，其余 $f(x)=x$
• Cantor’s Diagonal Argument：反证法（例：证明 $|(0,1)|\ne|\mathbb{Z}^+|$）
• 构造序列 $f(i)=0.b_{i1}b_{i2}b_{i3}\cdots$，则存在 $b_{ni}\ne b_{ii},f(n)\ne f(i)$ 对于任意 $i$，得证
• $\mathcal{P}(A)$ 为集合 $A$ 的所有子集的集合；$|A|<|\mathcal{P}(A)|$（设其双射，构造 $X=\{a:a\in A\text{ and } a\notin g(a)\}\in\mathcal{P}(A)$，应存在 $X=g(x)$，说明 $x$ 不存在以反证）
• 停机问题：不存在图灵机可解决之（假设图灵机 $P$，以及函数 $Halt(P,P)$）
• 集合可数：即 $|A|<\infty$ 或 $|A|=|\mathbb{Z}^+|$，否则不可数
• 集合可数无穷 $\Leftrightarrow$ 可以排成序列 $\Leftrightarrow$ 存在双射 $f:\mathbb{Z}^+\rightarrow A$
• 集合可数无穷，则任意无穷子集可数，$A\cup B, A\times B$ 也可数无穷
• 集合不可数，则其任意父集不可数
• Schröder-Bernstein Theorem：$|A|\le|B|,|B|\le|A|\Rightarrow|A|=|B|$
• $\aleph_0=|\mathbb{Z}^+|<2^{\aleph_0}=|\mathcal{P}(\mathbb{Z}^+)|=|[0,1)|=|(0,1)|=|\mathbb{R}|=c$
• The continuum hypothesis 连续统假设：不存在集合 $A$ 使得 $\aleph_0<|A|<c$

Lec11

• $r$-permutation 排列：$A$ 中 $r$ 个不同元素组成的序列
• 一个 $n$ 元素的集合有 $P(n,r)=A_n^r=\frac{n!}{(n-r)!}$ 种不同的 $r$-permutation
• 若为可重复 $r$-permutation 则有 $n^r$ 种
• multiset 多重集：某个元素 $x$ 出现了 $m$ 次则有重数 $m$，多重集 $A$ 有 $n$ 个元素为 $n$-multiset，$r$-subset 每个元素重数不超过父集
• 多重集的排列：先排列后去重 $\frac{(n_1+n_2+\cdots+n_k)!}{n_1!n_2!\cdots n_k!}$
• 普通集合 $r$-permutation 不带重复相当于 $\{1\cdot a_1,\cdots,1\cdot a_n\}$ 的排列，带重复相当于 $\{\infty\cdot a_1,\cdots,\infty\cdot a_n\}$ 的排列
• 最短路径：$p$ 行 $q$ 列格子，只能向右向上走，有 $\frac{(p+q)!}{p!q!}$ 种路径
• T-Route：斜着往右从 $(a,\alpha)$ 走到 $(b,\beta)$，需要满足 $b>a$; $b-a\ge|\beta-\alpha|$; $2\mid(b+\beta-a-\alpha)$
• T-Route 数量：

$$\frac{(b-a)!}{(\frac{b-a}{2}+\frac{\beta-\alpha}{2})!(\frac{b-a}{2}-\frac{\beta-\alpha}{2})!}$$

• 与 $x$ 轴相交的 T-Route 数量：即 $(a,-\alpha)$ 到 $(b,\beta)$ 的 T-Route 数量

$$\frac{(b-a)!}{(\frac{b-a}{2}+\frac{\beta+\alpha}{2})!(\frac{b-a}{2}-\frac{\beta+\alpha}{2})!}$$

• 不与 $x$ 轴相交的 T-Route 数量：即上面两者相减
• Bertrand’s Ballot Problem 投票问题：候选人 A, B 均获得 $n$ 张选票，在整个点票过程中 A 的票数都严格大于 $B$ 的概率是 $C_n/\binom{2n}{n}$，其中 $C_n$ 为卡特兰数
• Catalan Number 卡特兰数：下面方程组的解的个数，即从 $(1,2)$ 到 $(2n,1)$ 的 T-Route 个数

$$\begin{cases} x_1 + x_2 + \cdots + x_{2n} = n \\ x_1 + x_2 + \cdots + x_i \leq i/2, \quad i = 1,2,\dots,2n-1 \\ x_i \in \{0,1\}, \quad i = 1,2,\dots,2n \end{cases}$$

$$C_n=\frac{(2n-1)!}{(n-1)!n!}-\frac{(2n-1)!}{(n+1)!(n-2)!}=\frac{(2n)!}{n!(n+1)!}$$

Lec12

• $r$-combination 组合：一个集合的 $r$-subset （$r$-子集）
• 一个 $n$ 元素的集合有 $\binom{n}{r}=C_n^r=\frac{n!}{r!(n-r)!}$ 种不同的 $r$-combination
• 若为可重复 $r$-combination 则有 $\binom{n+r-1}{r}$ 种（相当于第 $i$ 个元素取 $x_i$ 个，$\sum x_i=r$）
• 将整数 $r$ 分为 $n$ 份（有顺序）有 $\binom{n+r-1}{r}$ 种分法（隔板法）
• $\mathcal{U}$ 为 $A=[n]$ 的所有带重复 $r$-组合 的集合，$\mathcal{V}$ 为 $[n+r-1]$ 的所有不带重复 $r$-组合 的集合
• 令 $U={u_1,\cdots,u_r}\in\mathcal{U}$，且 $1\le u_1\le u_2\le\cdots\le u_r\le n$，则 $1\le u_1<u_2+1<u_3+2<\cdots<u_r+r-1\le n+r-1$，而 ${u_1,u_2+1,\cdots,u_r+r-1}\in\mathcal{V}$；故 $f:\mathcal{U\rightarrow V}$ 构成双射，因此 $\mathcal{|U|=|V|}=\binom{n+r-1}{r}$
• 例：$\sum_{i_1=1}^n\sum_{i_2=1}^{i_1}\cdots\sum_{i_r=1}^{i_{r-1}} 1=\binom{n+r-1}{r}$，即生成最大值为 $n$ 的 $r$ 个元素的递增序列的个数
• 普通集合 $r$-combination 不带重复且 $0\le r\le n$ 相当于 $\{1\cdot a_1,\cdots,1\cdot a_n\}$ 的组合，带重复且 $r\ge 0$ 相当于 $\{\infty\cdot a_1,\cdots,\infty\cdot a_n\}$ 的组合，即 $\binom{n+r-1}{r}$
• 组合证明：$L=R$，同一对象用两种计数方式或构成双射
• 例 $\binom{n}{i}=\binom{n}{n-i}$：$X=\{s\in\{0,1\}^n:$ 包含 $i$ 个 $0$ $\}=\{s\in\{0,1\}^n:$ 包含 $n-i$ 个 $1$ $\}$
• $\{a_n\}_{n\ge s}$ 的二项式变换是 $\{b_n\}_{n\ge s}$ 并且 $b_n=\sum_{k=s}^n\binom{n}{k}a_k$
• Inverse Binomial Transform 二项式反演：$a_n=\sum_{k=s}^n(-1)^{n-k}\binom{n}{k}b_k$
• 引理：$\binom{n}{k}\binom{k}{i}=\binom{n}{i}\binom{n-i}{k-i}$，$\sum_{k=i}^n(-1)^{n-k}\binom{n}{k}\binom{k}{i}=\begin{cases}1\quad n=i\\0\quad n>i\end{cases}$
• 引理：令 $n,s\in\mathbb{N},s\le n$，则 $\sum_{k=s}^n\sum_{i=s}^ka_{k,i}=\sum_{k=s}^n\alpha_k=\sum_{i=s}^n\sum_{k=i}^na_{k,i}=\sum_{i=s}^n\beta_i$

$$\begin{array}{c|cccccc|c} k \backslash i & s & s+1 & s+2 & \cdots & n & \text{row sum} \\ \hline s & a_{s,s} & & & \cdots & & \alpha_s \\ s+1 & a_{s+1,s} & a_{s+1,s+1} & & \cdots & & \alpha_{s+1} \\ s+2 & a_{s+2,s} & a_{s+2,s+1} & a_{s+2,s+2} & \cdots & & \alpha_{s+2} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ n & a_{n,s} & a_{n,s+1} & a_{n,s+2} & \cdots & a_{n,n} & \alpha_n \\ \hline \text{col sum} & \beta_s & \beta_{s+1} & \beta_{s+2} & \cdots & \beta_n & \sum\sum \end{array}$$

Lec13

$$\begin{array}{|c|c|c|c|} \hline \text{object} & \text{box} & \text{formula} & \text{type} \\ \hline \text{labeled} & \text{labeled} & \frac{n!}{n_1! n_2! \dots n_k!} & \{n_1 \cdot 1, \dots, n_k \cdot k\} \text{ permutation} \\ \hline \text{unlabeled} & \text{labeled} & \binom{n+k-1}{n} & \{\infty \cdot 1, \dots, \infty \cdot k\} \text{ } n\text{-combination} \\ \hline \text{labeled} & \text{unlabeled} & \sum_{j=1}^{k} S_2(n,j) & \text{分类（相加），注意可空} \\ \hline \text{unlabeled} & \text{unlabeled} & \sum_{j=1}^{k} p_j(n) & \text{整数分割} \\ \hline \end{array}$$

• 第二类斯特林数（$n$ 个元素分成 $j$ 个非空集合）：$S_2(n,j)=\frac{1}{j!}\sum_{i=0}^{j-1}(-1)^i\binom{j}{i}(j-i)^n,n\ge j\ge 1$
• 证明：$T(n,j)$ 为将 $n$ 个区分的物品放入 $j$ 个区分的盒子（没有盒子空着）的方案数，$T(n,j)=j!\cdot S_2(n,j)$ ；$|X|=j^n$ 为有盒子空者的方案数；$X_i\subset X$ 有 $i$ 个盒子被使用的方案集合，${X_1,\cdots,X_j}$ 构成 partition，且 $|X_i|=\binom{j}{i}T(n,i)$ ，则 $j^n=|X|=\sum_{i=1}^j\binom{j}{i}T(n,i)$，二项式反演得出斯特林数公式
• 整数分割：把 $n$ 分成 $j$ 份方案数记为 $p_j(n)$；定理：$p_j(n+j)=\sum_{i=1}^jp_i(n)$ ；$p_1(n)=p_n(n)=1$；若 $j>n$ 则 $p_j(n)=0$
• Recurrence Relation 递推关系：Hanoi 塔问题 $H_1=1,H_2=3,H_n=2H_{n-1}+1$
• 线性齐次递推关系（LHRR）：$a_n=c_1a_{n-1}+c_2a_{n-2}+\cdots+c_ka_{n-k}$，有通项公式
• 特征根：LHRR 变换为 $r^k-c_1r^{k-1}-c_2r^{k-2}-\cdots-c_k=0$，可解得 $k$ 个特征根，再带回前 $k$ 个初始值 $a_n=c_1r_1^n+c_2r_2^n+\cdots+c_kr_k^n$，解出 $c_1,\cdots,c_k$；若特征根有重数 $m_{1},m_{2},\cdots,m_{t}$，则可构造通解：$x_{n}=\sum_{j=1}^k\left( \sum_{l=0}^{m_{j}-1} a_{j,l} n^l \right) r_{j}^n$
• 线性非齐次递推关系（LNRR）：$a_n=c_1a_{n-1}+c_2a_{n-2}+\cdots+c_ka_{n-k}+F(n)$ ；则 $a_n=$ 齐次通解 $+$ 特解
• LNRR 特解：若 $F(n)=P(n)s^n$，其中 $P(n)$ 为 $n$ 的 $l$ 阶多项式，$s$ 为特征根之一，其重数为 $m$，则特解 $x_n=(p_ln^l+\cdots+p_1n+p_0)s^nn^m$；齐次通解：两个不同特征根，则 $y_n = Ar_{1}^n+Br_{2}^n$；重根：$y_{n} = (A+Bn)r^n$ （参考上面）

Lec14

• $\{a_{r}\}_{r=0}^\infty$ 的生成函数 (Generating function) 为 $G(x)=\sum_{r=0}^\infty a_{r}x^r$；两个生成函数相等即每项相等
• 定义加减、数乘、乘法：$A(x)\cdot B(x)=\sum_{r=0}^\infty\left( \sum_{j=0}^r a_{j}b_{r-j} \right)$
• $A(x)$ 有逆元当且仅当 $a_0\ne0$ (如 $A(x)=\sum_{r=0}^\infty x^r$ 逆元为 $A^{-1}(x)=1-x$)
• Extended binomial coefficient: $u\in\mathbb{R},n\in\mathbb{N}$ 可定义

$$\binom{u}{n} = \begin{cases} \displaystyle \frac{u(u-1)\cdots(u - n + 1)}{n!} & n > 0 \\ 1 & n = 0 \end{cases}$$

• $x,u\in\mathbb{R},|x|<1$ 则 $(1+x)^u=\sum_{n=0}^\infty\binom{u}{n}x^n$；例如 $(1-\alpha x)^{-1}=\sum_{n=0}^\infty \alpha^n x^n$ 以及 $(1-\alpha x)^{-u}=\sum_{n=0}^\infty\binom{n+u-1}{n}a^nx^n$
• 两个多项式 $\deg(Q)>\deg(P),Q(x)=(1-r_{1}x)^{m_{1}}\cdots(1-r_{t}x)^{m_{t}}$ 则存在 $\frac{P(x)}{Q(x)} = \sum_{j=1}^t \sum_{u=1}^{m_{j}} \frac{a_{j,u}}{(1-r_{j}x)^u}$（可裂项）
• 使用生成函数解决 RR：例如 $a_n=8a_{n-1}+10^{n-1}$

$$\begin{aligned} A(x) &= \sum_{n=0}^\infty a_{n} x^n = 1 + \sum_{n=1}^\infty(8a_{n-1}+10^{n-1})x^n \\ &= 1 + 8xA(x) + \frac{x}{1-10x} \\ A(x) &= \frac{1-9x}{(1-8x)(1-10x)} = \frac{1}{2} \left( \frac{1}{1-8x} + \frac{1}{1-10x} \right) \\ &= \sum_{n=0}^\infty \frac{1}{2}(8^n+10^n)x^n \end{aligned}$$

• 卡特兰数 $C_n=C_{0}C_{n-1}+C_{1}C_{n-2}+\cdots+C_{n-1}C_{0}$ 生成函数 $xC(x)^2=C(x)-1$
• 用生成函数计算组合数：$a_n$ 为 $[k]$ 的带重复$n$-组合个数 (Type 2)，即 $N_i$ 为 $i$ 可能的出现次数的集合，$a_{n}=|\{(n_{1},\cdots,n_{k}):n_{1}\in N_{1},\cdots,n_k\in N_{k},n_{1}+\cdots+n_{k}=n\}|$
• $\sum_{n=0}^\infty a_{n}x^n=\sum_{n=0}^\infty\left( \sum_{n_{i}\in N_{i},n_{1}+\cdots+n_{k}=n}1 \right)x^n=\prod_{i=1}^k\sum_{n_{i}\in N_{i}}x^{n_{i}}$
• 例：$a_n$ 为分配 $n$ 本相同的书给 $5$ 个人，其中四人分别 $\ge3,\ge2,\ge4,\ge6$；则 $a_n=|\{(n_{1},\cdots,n_{5}):n_{1}\ge 3,\cdots,n_{5}\ge 0,n_{1}+\cdots+n_{5}=n\}|$，则

$$\begin{aligned} \sum_{n=0}^\infty a_{n}x^n&=(x^3+\cdots)\cdots(1+x+\cdots) \\ &=\frac{x^3}{1-x} \frac{x^2}{1-x} \cdots \frac{1}{1-x}=x^{15} \sum_{m=0}^\infty \binom{-5}{m}(-1)^m x^m \end{aligned}$$

• 计算 $[k]$ 的$n$-排列：$a_n=\sum \frac{n!}{n_{1}!n_{2}!\cdots n_{k}!}$；$\sum_{n=0}^\infty \frac{a_{n}}{n!} x^n = \prod_{i=1}^k \sum_{n_{i}\in N_{i}} \frac{x^{n_{i}}}{n_{i}!}$
• 例：$a_{n} = \{ s \in \{1,2,3,4\}^n:s \text{ has an even number of 1s} \}$

$$\begin{aligned} \sum_{n=0}^\infty \frac{a^n}{n!} x^n &= \left( 1 + \frac{x^2}{2!} + \frac{x^4}{4!}\cdots \right)\left( 1 + \frac{x}{1!} + \frac{x^2}{2!} + \cdots \right)^3 \\ &= \frac{e^x+e^{-x}}{2} \cdot e^{3x} = \frac{1}{2} \sum_{n=0}^\infty \left( \frac{4^n}{n!} + \frac{2^n}{n!} \right)x^n \end{aligned}$$

附录

• 泰勒级数

$$\begin{array}{ll} e^x=\sum^\infty_{n=0}\frac{x^n}{n!},& \ln(1+x)=\sum^\infty_{n=1}\frac{(-1)^{n-1}x^n}{n}\\ \sin x=\sum^\infty_{n=0}(-1)^{n}\frac{x^{2n+1}}{(2n+1)!},& \cos x=\sum^\infty_{n=0}(-1)^{n}\frac{x^{2n}}{(2n)!}\\ (1+x)^\alpha=\sum^\infty_{n=0}\frac{\alpha(\alpha-1)\cdots(a-n+1)}{n!}x^n \end{array}$$

• 组合数性质

$$\begin{array}{lll} \binom{n}{m}=\binom{n}{n-m} & \binom{n}{k}=\frac{n}{k}\binom{n-1}{k-1} & \binom{n}{m}=\binom{n-1}{m}+\binom{n-1}{m-1} \\ \sum_{i=0}^n\binom{n}{i}=2^n,[1] & \sum_{i=0}^n(-1)^i\binom{n}{i}=(n=0?),[2] & \binom{n}{r}\binom{r}{k}=\binom{n}{k}\binom{n-k}{r-k} \\ \sum_{i=0}^m\binom{n}{i}\binom{m}{m-i}=\binom{m+n}{m},n\ge m & \sum_{i=0}^n\binom{n}{i}^2=\binom{2n}{n} & \sum_{i=0}^n i\binom{n}{i}=n2^{n-1} \\ \sum_{i=0}^n i^2\binom{n}{i}=n(n+1)2^{n-2} & \sum_{l=0}^n\binom{l}{k}=\binom{n+1}{k+1},[3] & \sum_{i=0}^n\binom{n-i}{i}=F_{n+1},[4] \end{array}$$

• 1: 二项式定理的特殊情况 $a=b=1$；2: 特殊情况 $a=1,b=-1$，且 $n=0$ 答案为 $1$；3: 组合证明，取 $S={a_1,\cdots,a_{n+1}}$ 的 $k+1$ 子集数；4: $F$ 为斐波那契数列

下半学期

Lec15

• 命题：proposition；Simple Proposition, Compound(复合) Proposition, Propositional Constant, Propositional Variable, Propositional Logic
• Negation 否定 $\neg$，Conjunction 合取(and) $\land$，Disjunction 析取(or) $\lor$，Implication 蕴含 $\rightarrow$，Bi-Implication 等值 $\leftrightarrow$
• 蕴含的真值表：$p$ 为 T 时，$p\rightarrow q=q$，$p$ 为 F 时均为 T；等值：两者的真值相同为真
• Well-Formed Formulas(合式公式)：合法的公式，用树状结构检查
• 运算优先级：先括号，再依次为 $\neg, \land, \lor, \rightarrow, \leftrightarrow$，从左至右
• 转换例子：A comes to the party if and only if B doesn’t come, but, if B comes,
  then C doesn’t come and D comes. 答案：$(a\leftrightarrow\neg b)\land (b\rightarrow(\neg c\land d))$
• A sufficient condition for A coming to the party is that, if B does
  not come, then at least one of C and D must come. 答案：$(\neg b\rightarrow(c\lor d))\rightarrow a$

Lec16

• 真值表：如 $F=(p\rightarrow q)\land(q\rightarrow r)\leftrightarrow (p\rightarrow r)$，括号内分别为 $A,B,C$，则真值表头为 $p,q,r,A,B,C,A\land B,F$
• Tautology 重言式：任意truth assignment恒真；Contradiction 矛盾式：恒假；Contingency 可能式：非前面两者；Satisfiable：至少有一种真值指派使得它为真
• Logically Equivalent 逻辑等值：任意真值指派都有相同的真值；$A\equiv B$ 当且仅当 $A\leftrightarrow B$ 为 tautology
• 表格省略：交换律、结合律（括号内外同号）、分配律（异号）

$$\begin{array}{|c|c|} \hline \text{Double Negation Law 双重否定律} & \neg(\neg P) \equiv P \\ \hline \text{Identity Laws 同一律} & P \land \mathbf{T} \equiv P, P \lor \mathbf{F} \equiv P \\ \hline \text{Idempotent Laws 等幂律} & P \lor P \equiv P, P \land P \equiv P \\ \hline \text{Domination Laws 零律} & P \lor \mathbf{T} \equiv \mathbf{T}, P \land \mathbf{F} \equiv \mathbf{F} \\ \hline \text{Negation Laws 补余律} & P \lor \neg P \equiv \mathbf{T}, P \land \neg P \equiv \mathbf{F} \\ \hline \text{De Morgan's Laws 摩根律} & \neg(P \land Q) \equiv \neg P \lor \neg Q, \neg(P \lor Q) \equiv \neg P \land \neg Q \\ \hline \text{Absorption Laws 吸收律} & P \lor (P \land Q) \equiv P, P \land (P \lor Q) \equiv P \\ \hline P \to Q \equiv \neg P \lor Q & P \leftrightarrow Q \equiv (\neg P \lor Q) \land (P \lor \neg Q) \\ \hline P \to Q \equiv \neg Q \to \neg P & P \leftrightarrow Q \equiv (P \land Q) \lor (\neg P \land \neg Q) \\ \hline (P \to R) \land (Q \to R) \equiv (P \lor Q) \to R & P \leftrightarrow Q \equiv (P\rightarrow Q) \land (Q\rightarrow Q) \\ \hline P \to (Q \to R) \equiv (P \land Q) \to R & P \leftrightarrow Q \equiv \neg P \leftrightarrow \neg Q \\ \hline P \to (Q \to R) \equiv Q \to (P \to R) & \text{左侧为}\rightarrow\text{,右侧为}\leftrightarrow \\ \hline \end{array}$$

Lec17

• 若 $A^{-1}(\mathbf{T})$ 为令 $A$ 为 true 的真值指派，则 $A\equiv B \leftrightarrow A^{-1}(\mathbf{T})=B^{-1}(\mathbf{T})$，$\mathbf{T}$ 可换成 $\mathbf{F}$（即令命题为真或假的真值指派完全相同）
• Tautological Implication 重言蕴含 $\Rightarrow$：$A$ 重言蕴涵 $B$ 当任意真值指派使得 $A$ 为真时也会使得 $B$ 为真，即 $A^{-1}(\mathbf{T})\subseteq B^{-1}(\mathbf{T}),B^{-1}(\mathbf{F})\subseteq A^{-1}(\mathbf{F})$
• $A\Rightarrow B$ 当且仅当 $A\rightarrow B$ 是 tautology（即 $A$ 能推出 $B$），当且仅当 $A\land\neg B$ 是 contradiction

$$\begin{array}{|c|c|} \hline \text{Simplification 化简} & P \land Q \Rightarrow P \text{或} Q \\ \hline \text{Addition 附加} & P \Rightarrow P \lor Q \\ \hline \text{Modus ponens 假言推理} & P \land (P \rightarrow Q) \Rightarrow Q \\ \hline \text{Modus tollens 拒取} & \lnot Q \land (P \rightarrow Q) \Rightarrow \lnot P \\ \hline \text{Disjunctive syllogism 析取三段论} & \lnot P \land (P \lor Q) \Rightarrow Q \\ \hline \text{Hypothetical syllogism 假言三段论} & (P \rightarrow Q) \land (Q \rightarrow R) \Rightarrow (P \rightarrow R) \\ \hline \text{Resolution 归结} & (P \lor Q) \land (\lnot P \lor R) \Rightarrow (Q \lor R) \\ \hline \end{array}$$

• Argument 论证：一个命题序列，含有：Conclusion 结论，Premises 假设，Valid 有效（前提为真，则结论必为真），Proof 证明
• Argument Form 论证形式：一个 formula 公式序列，把 argument 中的命题换为命题 variables
• Rules of inference 推理规则：例题证明 $(P\lor Q)\land(P\rightarrow R)\land(Q\rightarrow S)\Rightarrow S\lor R$

$$\begin{array}{ll} (1)\quad P \lor Q & \text{Premise} \\ (2)\quad \lnot P \rightarrow Q & \text{Rule of replacement applied to (1)} \\ (3)\quad Q \rightarrow S & \text{Premise} \\ (4)\quad \lnot P \rightarrow S & \text{Hypothetical syllogism applied to (2) and (3)} \\ (5)\quad \lnot S \rightarrow P & \text{Rule of replacement applied to (4)} \\ (6)\quad P \rightarrow R & \text{Premise} \\ (7)\quad \lnot S \rightarrow R & \text{Hypothetical syllogism applied to (5) and (6)} \\ (8)\quad S \lor R & \text{Rule of replacement applied to (7)} \\ \end{array}$$

Lec18

• Predicate 谓词：一元(Unary)谓词，如 $5$ 是整数；二元(Binary)谓词，如 $a$ 比 $b$ 大；Predicate constant，Predicate variable；Individual 个体词：你在考虑的东西；Individual constant：如 $5$，Individual variable：如 $a$；Domain 个体域：所有被考虑的个体的集合
• Propositional function 命题函数：$P(x_1,\dots,x_n)$，$P$ 是 $n$ 元谓词；如 $p$ 为 Alice’s father is a doctor，$f(x)=x$’s father，谓词 $D$ 为 is a doctor，则 $p=D(f(Alice))$
• Universal Quantifier 全称量词 $\forall$，如 $\forall xP(x)$；Existential Quantifier 存在量词 $\exists$
• 如果 $\forall,\exists$ 被用于个体 variable $x$，则其为 bound 约束的，否则是 free 自由的
• Well-Formed Formulas 合式公式：正确且包含上述内容及表达式；WFF 类型：logically valid 普遍有效，恒真；unsatisfiable 不可满足，恒假；satisfiable 可满足，存在真的情况
• 转换例子：There is a symbol that can not be understood by any person’s brain. $S(x)$: $x$ is a symbol. $P(x)$: $x$ is a person. $U(x,y)$: x can understand y. $b(x)$ the brain of $x$. 答案：$\exists x(S(x)\land \forall y(P(y)\rightarrow \neg U(b(y),x)))$
• Interpretation 解释：把所有变量换成实际的东西；Logical Equivalence 逻辑等值：任意解释都有相同的真值（类比任意真值指派）

Lec19

$$\begin{array}{|c|c|} \hline \text{De Morgan's Laws 摩根律} & \neg \forall xP(x) \equiv \exists x \neg P(x), \neg \exists xP(x) \equiv \forall x \neg P(x)\\ \hline \text{Distributive Laws 分配律} & \forall x(P(x)\land Q(x))\equiv \forall x P(x)\land \forall x Q(x) \\ & \exists x(P(x)\lor Q(x))\equiv \exists x P(x)\lor \exists x Q(x) \\ \hline \text{Conclusion Premise 附加前提} & P\Rightarrow A\rightarrow B \equiv P\land A \Rightarrow B \\ \hline \forall x P(x)\lor \forall x Q(x) \Rightarrow \forall x(P(x)\lor Q(x)) & \exists x(P(x)\land Q(x))\Rightarrow \exists x P(x)\land \exists x Q(x) \\ \hline \forall x (P(x) \rightarrow Q(x)) \Rightarrow \forall x P(x) \rightarrow \forall x Q(x) & \forall x (P(x) \rightarrow Q(x)) \Rightarrow \exists x P(x) \rightarrow \exists x Q(x)\\ \hline \forall x (P(x) \leftrightarrow Q(x)) \Rightarrow \forall x P(x) \leftrightarrow \forall x Q(x) & \forall x (P(x) \leftrightarrow Q(x)) \Rightarrow \exists x P(x) \leftrightarrow \exists x Q(x)\\ \hline \forall x (P(x) \rightarrow Q(x)) \land P(a) \Rightarrow Q(a) & \forall x (P(x) \rightarrow Q(x)) \land \forall x (Q(x) \rightarrow R(x)) \\ & \Rightarrow \forall x (P(x) \rightarrow R(x))\\ \hline \text{Universal Instantiation 全称量词消去} & \forall x P(x) \Rightarrow P(a) \\ & a \text{ is any individual in the domain of } x \\ \hline \text{Universal Generalization 全称量词引入} & P(a) \Rightarrow \forall x P(x) \\ & a \text{ takes any individual in the domain of } x \\ \hline \text{Existential Instantiation 存在量词消去} & \exists x P(x) \Rightarrow P(a) \\ & a \text{ is a specific individual in the domain of } x \\ \hline \text{Existential Generalization 存在量词引入} & P(a) \Rightarrow \exists x P(x) \\ & a \text{ is a specific individual in the domain of } x \\ \hline \end{array}$$

• 例题：$\exists x (C(x) \land \neg B(x)) \land \forall x (C(x) \rightarrow P(x)) \Rightarrow \exists x (P(x) \land \neg B(x))$

$$\begin{array}{ll} (1)\quad \exists x (C(x) \land \neg B(x)) & \text{Premise} \\ (2)\quad C(a) \land \neg B(a) & \text{Existential instantiation from (1)} \\ (3)\quad C(a) & \text{Simplification from (2)} \\ (4)\quad \forall x (C(x) \rightarrow P(x)) & \text{Premise} \\ (5)\quad C(a) \rightarrow P(a) & \text{Universal instantiation from (4)} \\ (6)\quad P(a) & \text{Modus ponens from (3) and (5)} \\ (7)\quad \neg B(a) & \text{Simplification from (2)} \\ (8)\quad P(a) \land \neg B(a) & \text{Conjunction from (6) and (7)} \\ (9)\quad \exists x (P(x) \land \neg B(x)) & \text{Existential generalization from (8)} \\ \end{array}$$

Lec20

• 图 $G=(V,E)$ 即 edges 和 vertices，$|V|$ 为 $G$ 的 order 阶数

$$\begin{array}{|c|c|c|c|} \hline \text{Type} & \text{Edges} & \text{Multiple Edges Allowed?} & \text{Loops Allowed?} \\ \hline \text{Simple graph} & \text{undirected} & \text{No} & \text{No} \\ \hline \text{Multigraph} & \text{undirected} & \text{Yes} & \text{No} \\ \hline \text{Pseudograph} & \text{undirected} & \text{Yes} & \text{Yes} \\ \hline \text{Simple directed graph} & \text{directed} & \text{No} & \text{No} \\ \hline \text{Directed multigraph} & \text{directed} & \text{Yes} & \text{Yes} \\ \hline \text{Mixed graph} & \text{undirected + directed} & \text{Yes} & \text{Yes} \\ \hline \end{array}$$

• Adjacency List 邻接表；Adjacency Matrix 邻接矩阵（开 $n$ 方则为从节点 $i$ 到节点 $j$ 的长度为 $n$ 的路径条数）；Incidence Matrix 关联矩阵（行是点，列是边）；isolated $\deg(v)=0$；pendant 悬挂的 $\deg(v)=1$
• Handshaking Theorem：无向图，$2|E|=\sum_{v\in V}\deg(v)$，并且 $|\{v\in V:\deg(v)\text{为奇数}\}|$ 为偶数；有向图，$\sum_{v\in V}\deg^-(v)=\sum_{v\in V}\deg^+(v)=|E|$
• proper subgraph 真子图；subgraph induced 导出子图（$W\subseteq V,W=\{1,2,3,4\},G'=G[W]$ 或 $F\subseteq E,F=\{\{1,2\},\{2,3\}\},G''=G[F]$）；Edge Contraction 即合并两个点；complement graph 补图，补成完全图（$K_n$）；Isomorphism 同构，即连接方式一样（顶点编号无关）

Lec21

• 一个简单图是二分图 $K_{n,n}$ 当且仅当存在一种可能的着色方案，使得任意两个相邻顶点不同色；Matching 匹配（仅二分图，是边的集合）；
• Hall’s Theorem：二分图 $G=(X\cup Y,E)$ 有完全匹配当且仅当 $\forall A\subseteq X,|N(A)|\ge|A|$ （$N(A)$ 是邻接集，和 $A$ 相连点的集合）
• Path：简单 simple 路径不经过一个边超过两次；passes through 点，traverses 边
• connected 连通的：即任意两个不同点之间都有 path
• Connected Component 连通分支/分量：即极大连通子图（类似森林的不同树）

Lec22

• Cut vertex割点，Cut edge(bridge) 割边，即去除后就有了更多的连通分量
• Vertex Connectivity 点连通度 $\kappa(G)$：nonseparable 不可分的，即没有割点；对于一个连通简单图，vertex cut 点割集即去掉这些点后变成不连通；点连通度，即点割集点数量的最小值（非连通图为 $0$，完全图为 $n-1$）；一个图是 $k$-连通的当 $\kappa(G)\ge k$
• Edge Connectivity 边连通度 $\lambda(G)$：非连通图 $\lambda(G)=0$，连通图 $|V|=1$ 时 $\lambda(G)=0$，否则为边割集（edge cut）边数量的最小值
• $\delta(G)=\min_{v\in V}\deg(v)$，则 $\kappa(G)\le \lambda(G)\le \delta(G)$
• Strongly/Weakly Connected：有向图，分别为考虑方向/不考虑方向的连通
• 长度大于3的简单回路是同构不变量
• Euler Path/Circuit 欧拉路径/回路：simple path/circuit 遍历每个边
• 欧拉回路：$G$ 为连通的点数大于 2 的 multigraph，存在欧拉回路当且仅当对任意点 $v$ 都有 $2|\deg(v)$
• Hierholzer 算法：先选择一个环，将图不断去掉这个环和孤立的点，再选取图中的一个与当前环有某个点重合的环，再把两个环拼接，循环，最后得到欧拉回路
• 欧拉路径：$G$ 为连通的点数大于 2 的 multigraph，存在欧拉路径当且仅当 $G$ 恰好有两个点有奇数的度；算法：连接这两个奇数度的点，用 Hierholzer，再去除该边

Lec23

• 欧拉是遍历边，哈密顿 Hamilton 是遍历点
• 哈密顿回路存在充分条件: Ore’s Theorem: 点数大于 3 的简单图，如果 $\forall\{u,v\}\notin E,\deg(u)+\deg(v)\ge n$；Dirac’s Theorem：点数大于 3 的简单图，如果对任意点都有 $\deg(u)\ge \frac{n}{2}$
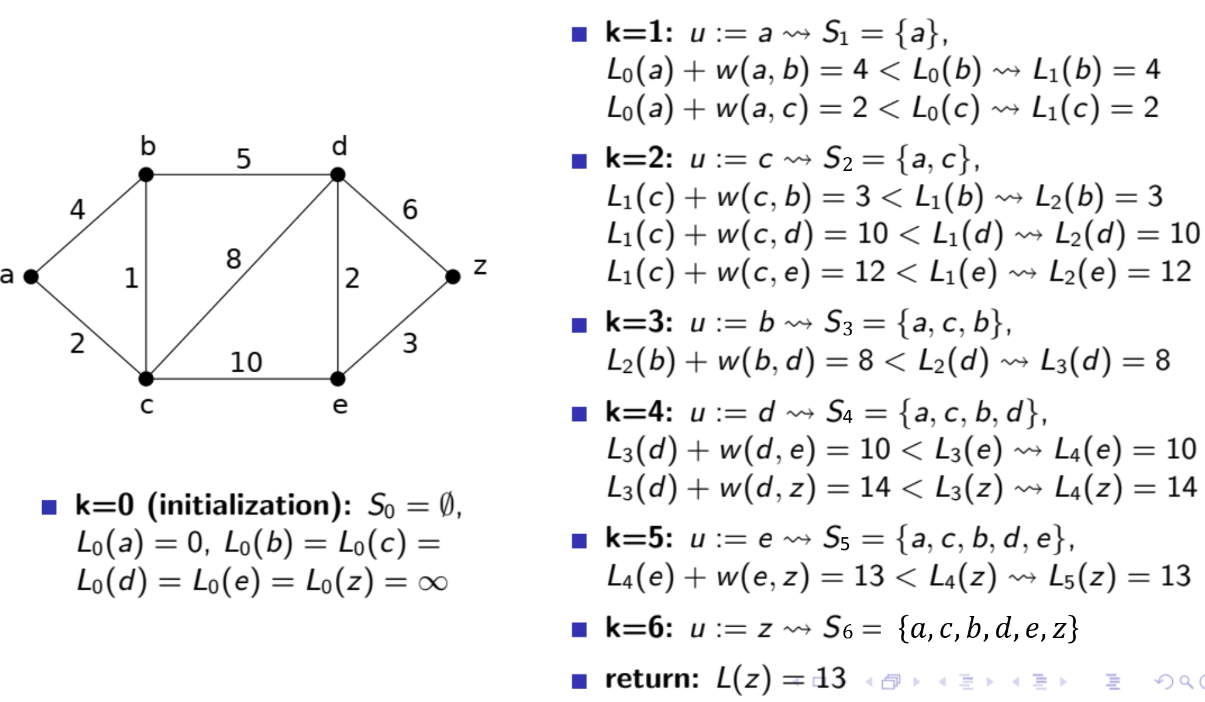
• Djikstra’s Algorithm：

Lec24

• Planar Graph 平面图：可以被画在平面上且没有边相交
• Jordan Curve Theorem：简单闭合平面曲线把平面分为内外区域，连接这两个区域的曲线一定和该曲线相交；图 $K_{3,3}$ 判断方法：先选择一个环，再依次画边，如果有哪条边跨区域了就非平面
• Regions 面：平面图划分出来的多个区域，有 exterior 外部面，boundary，degree（一个面的边界上边的数量）
• Euler’s Formula：对于连通简单平面图，面的数量 $r=e-v+2$；有 $p$ 个连通分量：$r=e-v+p+1$
• 一个平面连通简单图，如果每个面的度都大于 $l$，则 $|E(G)|\le \frac{l}{l-2}(|V(G)|-2)$
• Homeomorphic 同胚的：同一个图经过不同的 elementary subdivision 初等细分（拆分一条边为两条）后获得的图
• Kuratowski’s Theorem：一个图是非平面的当且仅当其有一个子图和 $K_{3,3}$ 或 $K_5$ 同胚
• Dual Graph 对偶图：一个平面图，面变成点，点变成面后得到 $G^*$；有 $2v-2$ 条边，$G^{**}=G,v^*=f,e^*=e,f^*=v$（$f$ 为面）；self-dual 即某个图的对偶图和它本身同构

Lec25

• chromatic number $\chi(G)$ 色数：$k$-着色的最小 $k$ 值；$1\le \chi(G)\le |V|$（平面图不超过4色）
• $\chi(G) = 1$ iff $E = \emptyset$；$\chi(G) = 2$ iff $G$ is bipartite and $|E| \ge 1$
• $\chi(K_n) = n$ for every integer $n \ge 1$；$\chi(G) \ge n$ if $G$ has a subgraph isomorphic to $K_n$
• $\chi(C_n) = 2$ if $2|n$; $\chi(C_n) = 3$ if $2|(n-1)$; ($n \ge 3$)
• $\chi(G) \le \Delta(G) + 1$, where $\Delta(G) = \max\{\deg(v): v \in V\}$
• 树的定义：无向无环图里两个点之间有唯一路径；$n$ 顶点的树有 $n-1$ 边；Rooted Tree（有向树）；full $m$-ary tree：叶子是满的，$n=mi+1$

Lec26

• Preorder/Inorder/Postorder traversal; Prefix/Infix/Postfix notation
• Spanning tree 生成树：一个简单图含有生成树当且仅当其连通
• Prim’s Algorithm：选取一个点开始，选取与当前树连接的最小权边
• Kruskal’s Algorithm：初始每个点自成一个 component，循环地选取最小权边并 merge 两个 components（除非成环）

Lec27

• Language: 可被自动机 $M_1$ 识别的字符串的集合记为 $A=L(M_1)$，如果一个语言能被某个有限自动机识别，则语言 regular 正则
• 有限自动机 $M$ 为五元组 $(Q,\Sigma,\delta,q_0,F)$：$Q$ 为有限状态集合，$\Sigma$ 为有限字母表集合，$\delta$ 为转换方程 $\delta:Q\times\Sigma\rightarrow Q$ 如 $\delta(q,a)=r$ 意味着从 $q$ 匹配字符 $a$ 到状态 $r$，$q_0$ 为初始状态，$F$ 为可接受的状态集合
• Union $\cup$，Concatenation $A\circ B=AB$，Star $A^*=\{\epsilon,a,b,aa,ab,ba,aab,\dots\}$
• Regular Expression：从字符集、空集和 $\epsilon$ 通过上述三个符号构建成
• 正则语言的封闭性质：两个正则语言 $A_1\cup A_2$：$Q=Q_1\times Q_2, q_0=(q_1,q_2),\delta((q,r),a)=(\delta_1(q,a),\delta_2(r,a))$, $F=(F_1\times Q_2)\cup(Q_1\times F_2)$；或者用 NFA 在最前面加入初始状态，用 $\epsilon$ 连接两个自动机的初始状态
• 两个正则语言 $A_1\circ A_2$：把第一个的可接受状态用 $\epsilon$ 连到第二个的初始状态
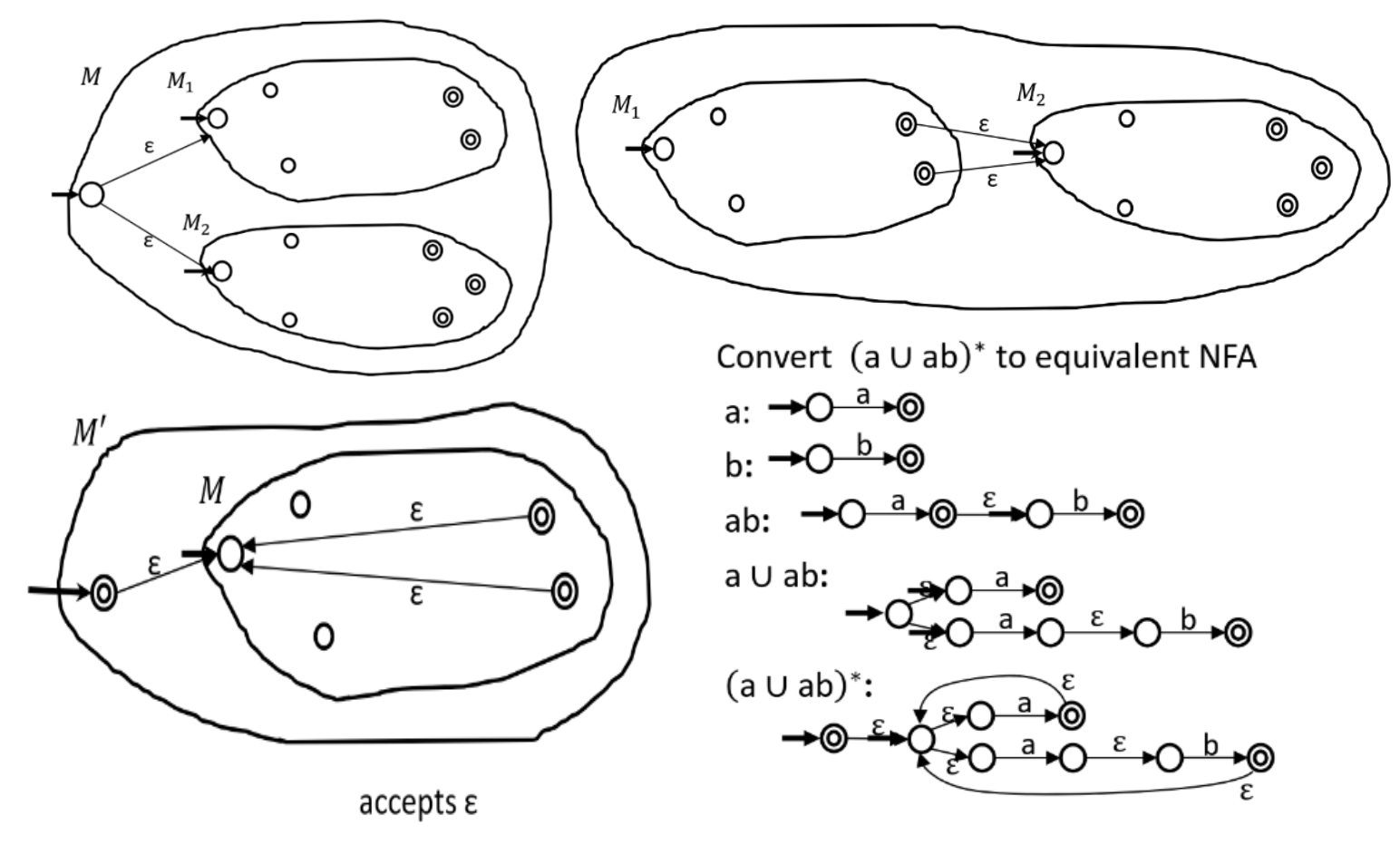
• Nondeterministic Finite Automata：允许接受 $\epsilon$，不消耗字符，$\delta$ 右侧变为状态集合
• NFA $M$ 转为 DFA $M'$：$Q'=\mathbf{P}(Q),q'_0=\{q_0\},F'=\{R\in Q'|R \text{ intersects } F\}$
• $A_1\cup A_2,A_1A_2,A^*$ 的自动机：

Lec28

• Generalized NFA：状态之间转换从字符变成正则表达式；每个 GNFA 都有等价的正则表达式（对状态数 $k$ 从 $2$ 开始归纳法，每个 $k$ states GNFA 都能转换成 $k-1$ 的 GNFA）
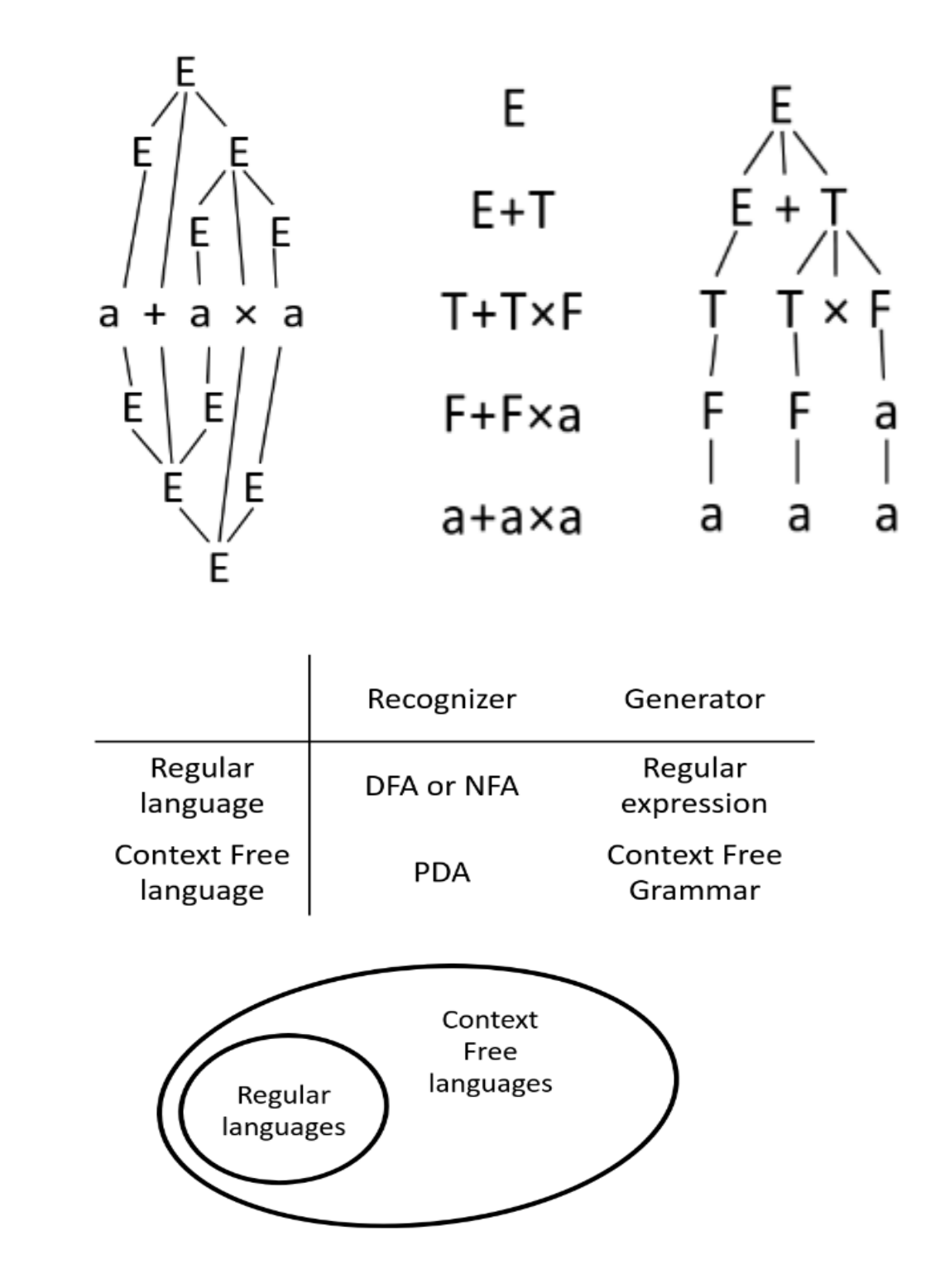
• Context Free Grammars：四元组 $(V,\Sigma,R,S)$，$V$ 是变量有限集合，$\Sigma$ 是 terminal symbols 终止符集合，$R$ 是规则集合（形式 $V\rightarrow (V\cup\Sigma)^*$），$S$ 是初始变量
• $u,v\in (V\cup \Sigma)^*$，如果 $u$ 仅用一次 subtitution 走到 $v$ 记为 $u\Rightarrow v$；如果多次记为 $u \overset{*}{\Rightarrow}v$（derivation）；Context Free Language 如果 $A=L(G)$
• 例子：$G_2$，$E\rightarrow E+T|T,T\rightarrow T\times F|F,F\rightarrow(E)|a$；$G_3$，$E\rightarrow E+E|E\times E|(E)|a$
• 虽然 $L(G_2)=L(G_3)$ 但是 $G_2$ 不模糊（表达了符号顺序），$G_3$ 模糊
• Pushdown Automata：外接一个栈，如识别 $D=\{0^k1^k|k\ge0\},B=\{ww^R|w\in\{0,1\}^*\}$ （1. 读入并压栈，重复或去2；2. 读入并 pop，比较如果当前的不等于上一个，则拒绝；3. 栈为空进入接受状态），为六元组 $(Q,\Sigma,\Gamma,\delta,q_0,F)$，$\Sigma,\Gamma$ 分别为输入/栈的字母，$\delta:Q\times\Sigma_\epsilon\times\Gamma_\epsilon\rightarrow\mathcal{P}(Q\times\Gamma_\epsilon)$，$\delta(q,a,c)=\{(r_1,d),(r_2,e)\}$
• CFG 转为 PDA：Push the start symbol on the stack, If the top of stack is Variable: replace with right hand side of rule (nondet choice). Terminal: pop it and match with next input symbol. If the stack is empty, accept.
•